Largest region in the matrix – DFS & BFS
If you have or had troubles understanding breath or depth first search, you’ve come to the right place. Here it is – recursive graph search made easy.
Depth-First Search
Depth-first search (DFS) is a method for exploring a graph. In a DFS, you follow the child of traversing node, meaning if the current node has a child, with each step you’ll go deeper into the graph in terms of distance from the root. If a node hasn’t any unvisited children, then go up one level to parent.
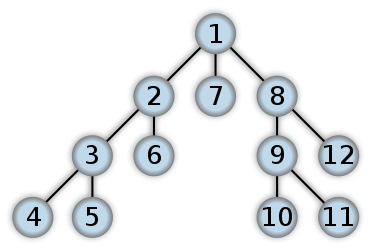
Breadth-First Search
Breadth-first search (BFS) is a method for exploring a graph. In a BFS, you first explore all the nodes one step away from the root, then all the nodes two steps away, etc.
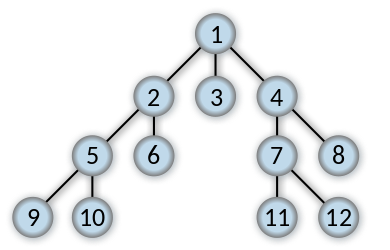
The Problem
Consider a matrix with rows and columns, where each cell contains either a ‘0’ or a ‘1’ and any cell containing a 1 is called a filled cell. Two cells are said to be connected if they are adjacent to each other horizontally, vertically, or diagonally. If one or more filled cells are also connected, they form a region. find the length of the largest region.
Input : M[][5] = { 0 0 1 1 0
1 0 1 1 0
0 1 0 0 0
0 0 0 0 1 }
Output : 6
Ex: in the following example, there are 2 regions one with length 1 and the other as 6.
The largest region : 6