Points lying inside a circle – duplicated point variation
Given three parameters of equal size:
- string S – points names (duplicates allowed)
- int[] X – point coordinate
- int[] Y – point coordinate
Calculate the number of points lying within the circle ranging to the closest duplicated point excluding points crossing the edge of the circle.
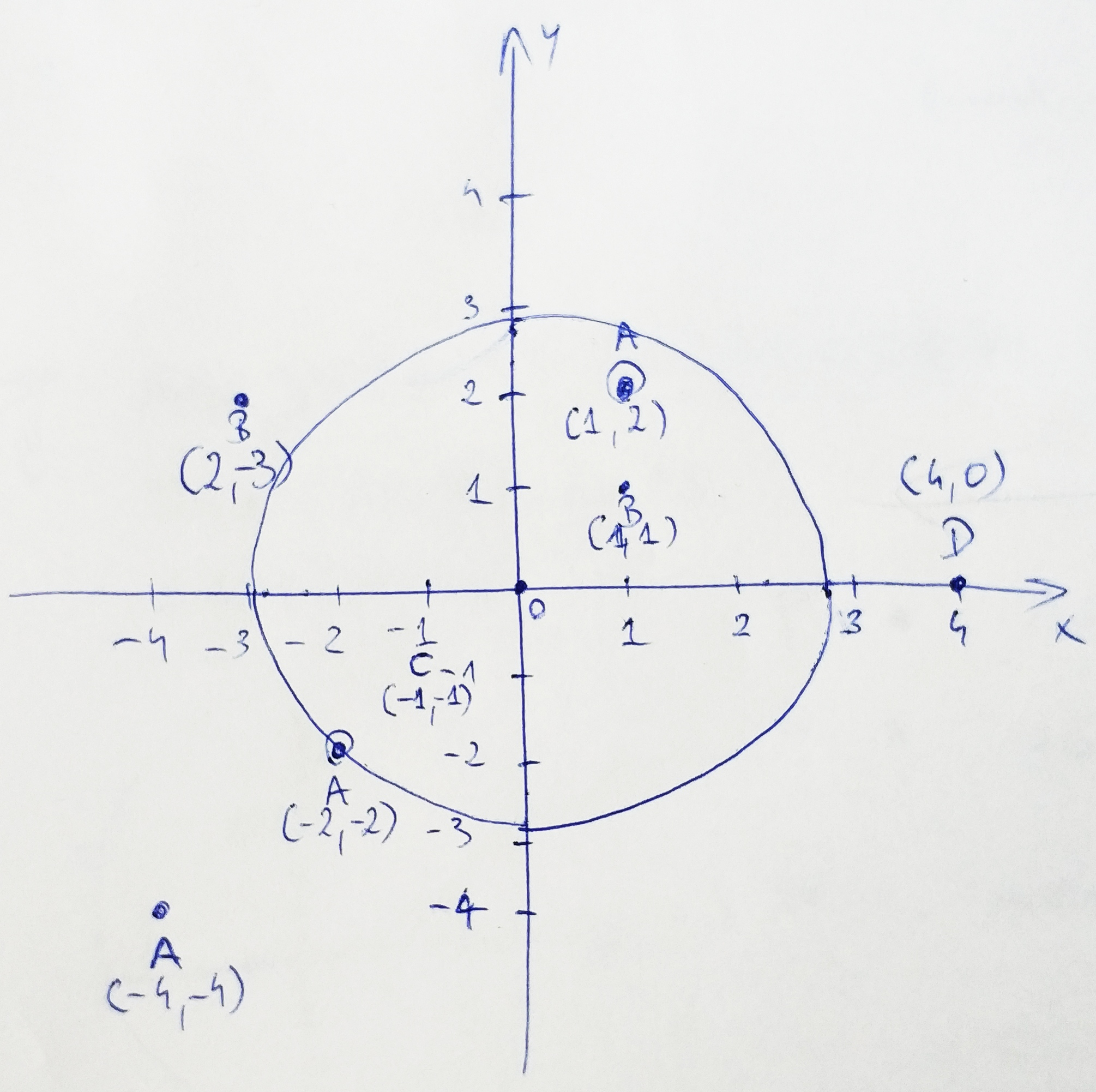
Looking at the chart, the points we are interested in: B (1, 1), A (1, 2) and C (-1,-1). Point A (-2, -2) is excluded because it lies on the circle’s edge. Circle radius is determined upon the closest duplicated point. There are two sets of duplicated points on the above chart: B – ([2, -3], [1,1] and A – ([-2, -2], [1, 2], [-4, -4]).
Solution:
This task is quite easy once you understand that the sign of the coordinates doesn’t matter.
First, let’s start by adding a check if we have any duplicated point groups:
public static int getResult(string S, int[] X, int[] Y)
{
if (S.Distinct().Count() == S.Count())
return 0;
}Secondly, we need to calculate the distance of each point from the center of the plane by using Pythagorean theorem:
Let’s extract it to another method:
private static decimal getPointHypotenuse(int x, int y)
{
return (decimal)Math.Sqrt((Math.Pow(x, 2) + Math.Pow(y, 2)));
}public static int getResult(string S, int[] X, int[] Y)
{
if (S.Distinct().Count() == S.Count())
return 0;
List<Tuple<char, decimal>> list = new List<Tuple<char, decimal>>();
for (int i = 0; i < S.Length; i++)
{
list.Add(new Tuple<char, decimal>(S[i], getPointHypotenuse(X[i], [i])));
}
}Next, since we can have N number of any type of point, let’s group them together in a sorted list:
var aggregated = list.GroupBy(x => x.Item1)
.Where(x => x.Count() > 1)
.Select(g => Tuple.Create(g.Key, g.Min(t => t.Item2)))
.OrderBy(x => x.Item2)
.ToList();The last step is to pick the second lowest number from any of the groups and filter the list of points with their distances to include only points below the limit.
Here’s the full listing:
public static class PointsWithinACircle
{
public static int getResult(string S, int[] X, int[] Y)
{
if (S.Distinct().Count() == S.Count())
return 0;
List<Tuple<char, decimal>> list = new List<Tuple<char, decimal>>();
for (int i = 0; i < S.Length; i++)
{
list.Add(new Tuple<char, decimal>(S[i], getPointHypotenuse(X[i], Y[i])));
}
var aggregated = list.GroupBy(x => x.Item1)
.Where(x => x.Count() > 1)
.Select(g => Tuple.Create(g.Key, g.Min(t => t.Item2)))
.OrderBy(x => x.Item2)
.ToList();
var result = (from s in list
join a in aggregated on s.Item1 equals a.Item1
where s.Item2 > a.Item2
orderby s.Item2
select (s.Item1, s.Item2)).First();
var numberOfPoints = list.Where(x => x.Item2 < result.Item2).Count();
return numberOfPoints;
}
private static decimal getPointHypotenuse(int x, int y)
{
return (decimal)Math.Sqrt((Math.Pow(x, 2) + Math.Pow(y, 2)));
}
}