Points lying inside a circle – duplicated point variation
Given three parameters of equal size:
- string S – points names (duplicates allowed)
- int[] X – point coordinate
- int[] Y – point coordinate
Calculate the number of points lying within the circle ranging to the closest duplicated point excluding points crossing the edge of the circle.
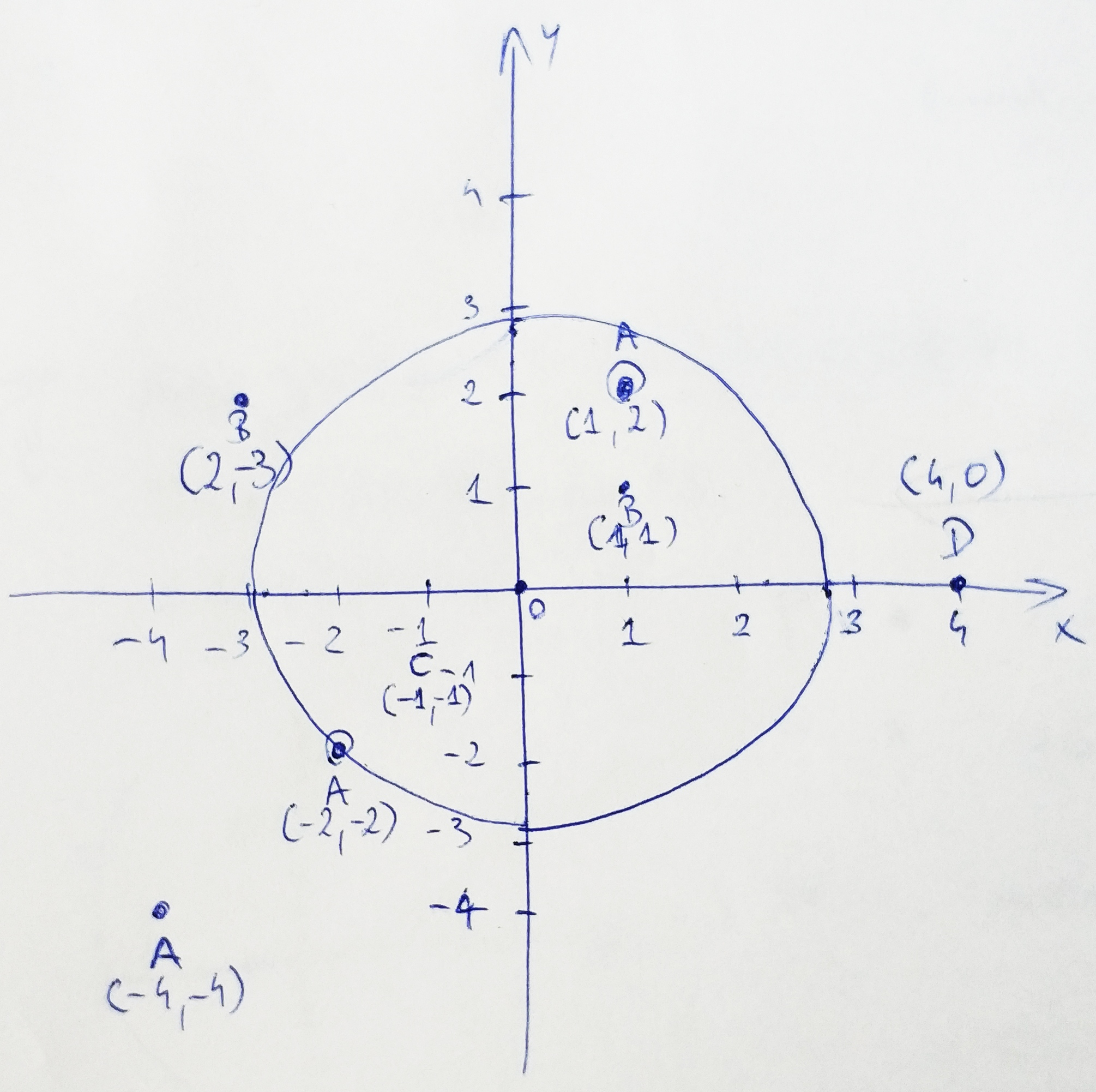
Looking at the chart, the points we are interested in: B (1, 1), A (1, 2) and C (-1,-1). Point A (-2, -2) is excluded because it lies on the circle’s edge. Circle radius is determined upon the closest duplicated point. There are two sets of duplicated points on the above chart: B – ([2, -3], [1,1] and A – ([-2, -2], [1, 2], [-4, -4]).
Solution:
This task is quite easy once you understand that the sign of the coordinates doesn’t matter.
First, let’s start by adding a check if we have any duplicated point groups:
public static int getResult(string S, int[] X, int[] Y)
{
if (S.Distinct().Count() == S.Count())
return 0;
}Secondly, we need to calculate the distance of each point from the center of the plane by using Pythagorean theorem:
Let’s extract it to another method:
private static decimal getPointHypotenuse(int x, int y)
{
return (decimal)Math.Sqrt((Math.Pow(x, 2) + Math.Pow(y, 2)));
}public static int getResult(string S, int[] X, int[] Y)
{
if (S.Distinct().Count() == S.Count())
return 0;
List<Tuple<char, decimal>> list = new List<Tuple<char, decimal>>();
for (int i = 0; i < S.Length; i++)
{
list.Add(new Tuple<char, decimal>(S[i], getPointHypotenuse(X[i], [i])));
}
}Next, since we can have N number of any type of point, let’s group them together in a sorted list:
var aggregated = list.GroupBy(x => x.Item1)
.Where(x => x.Count() > 1)
.Select(g => Tuple.Create(g.Key, g.Min(t => t.Item2)))
.OrderBy(x => x.Item2)
.ToList();The last step is to pick the second lowest number from any of the groups and filter the list of points with their distances to include only points below the limit.
Here’s the full listing:
public static class PointsWithinACircle
{
public static int getResult(string S, int[] X, int[] Y)
{
if (S.Distinct().Count() == S.Count())
return 0;
List<Tuple<char, decimal>> list = new List<Tuple<char, decimal>>();
for (int i = 0; i < S.Length; i++)
{
list.Add(new Tuple<char, decimal>(S[i], getPointHypotenuse(X[i], Y[i])));
}
var aggregated = list.GroupBy(x => x.Item1)
.Where(x => x.Count() > 1)
.Select(g => Tuple.Create(g.Key, g.Min(t => t.Item2)))
.OrderBy(x => x.Item2)
.ToList();
var result = (from s in list
join a in aggregated on s.Item1 equals a.Item1
where s.Item2 > a.Item2
orderby s.Item2
select (s.Item1, s.Item2)).First();
var numberOfPoints = list.Where(x => x.Item2 < result.Item2).Count();
return numberOfPoints;
}
private static decimal getPointHypotenuse(int x, int y)
{
return (decimal)Math.Sqrt((Math.Pow(x, 2) + Math.Pow(y, 2)));
}
}Reordering DataTable Optimization Use Case
Scenario
Let’s assume we have a header based import accepting CSV files, with the following criteria:
- columns can be placed in a file in any order
- any number of columns can be added to an import file
- there can be a variable number of XML columns, which should be translated to a valid XML and placed in a single column matching SQL bulk insert table
- the service should output a DataTable with a schema matching bulk insert table with buckets in XML format
Ok, so we have two types of column:
- simple column, which should be validated and mapped to an existing DB column from a table, to which we’ll be performing a bulk insert
- xml columns, which should be translated to a valid xml and merged into one, because there’s a single xml column in bulk insert table, to which we need to insert
Problem
What’s the problem with this kind of design? First, which comes to my mind is that the xml column in bulk table (it could be json, doesn’t matter) adds verticality to the data storage, which means that sql won’t be able to use simple joins. It also requires parsing the data both ways and, since we don’t know how many xml columns will be included in the import file, it’s difficult to avoid n^2 complexity.
Morever, we get a initial DataTable with a different schema compared to the target DataTable. In the initial DataTable all columns were stored in a string format. We need to fetch the schema and modify the first DataTable.
Expected size of data- 100,000 rows, up to 50 XML columns. In this example I’ll omit the validation part and focus on the reordering service performance.
Initial approach
- We fetched the bulk insert table schema and created a new DataTable object
- For each source table row, a new DataRow was created
- Another for loop iterated through the source rows’ columns
- In the second loop we were checking the correct name of the column and copying value from source table
_destinationDataTable = await _dataSchemaService.GetTemplateSchema(tableName);
for (var row = 0; row < source.Rows.Cast<DataRow>().Count(); row++)
{
var newRow = _destinationDataTable.NewRow();
var xmlBucket = new RateBucketsOverride();
for (var index = 0; index < source.Columns.Count; index++)
{
var cellValue = source.Rows[row].ItemArray[index].ToString();
if (!string.IsNullOrWhiteSpace(cellValue))
{
var columnInfo =
mappedfields.First(c => c.SourceColumn == source.Columns[index].ColumnName);
if (columnInfo.Mapped)
{
var column = GetDataColumn(columnInfo.DbDestinationColumn);
newRow[column] = cellValue;
}
else
{
xmlBucket.BucketOverrides.Add(new BucketOverride
{BucketDescription = columnInfo.SourceColumn, BucketOverrideValue = cellValue});
}
}
}
if (xmlBucket.BucketOverrides.Count > 0) AddBucketsToRow(xmlBucket, newRow);
if (newRow.ItemArray.Length > 0)
_destinationDataTable.Rows.Add(newRow);
}
AddFileName(fileName);Closer look
Ok, the code works and passes all unit tests. What’s wrong with it?
- Whole table coppied every time, row by row, column by column
- Double LINQ string-based column name checking
- OK performance for small to medium number of rows (<5000)
Computional complexity:
(2n+1)*(3*m + 4)=> n*m
Additionally, it turned out during the test that type casting in the outer loop had horrific extreme negative impact on performance.
for (var row = 0; row < source.Rows.Cast<DataRow>().Count(); row++)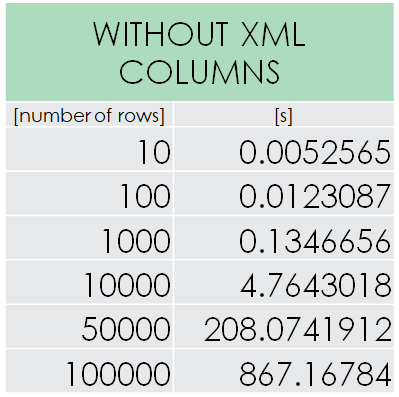 This is the performance of the initial solution. ~14m30s for 100,000 rows is hugely disappoiting and shows how quickly things can go sideways. The duration increase approximately matches expected complexity. Since the whole table is rebuild, it doesn’t matter if there are any XML rows or now. It’s always the worst case scenario. What can we do about it?
This is the performance of the initial solution. ~14m30s for 100,000 rows is hugely disappoiting and shows how quickly things can go sideways. The duration increase approximately matches expected complexity. Since the whole table is rebuild, it doesn’t matter if there are any XML rows or now. It’s always the worst case scenario. What can we do about it?
Using Table Merge
- I added unit tests to check the solution validity
- Performance tests were added to measure the execution time
- Code was refactored into smaller functions for readability
- Instead of creating new table, all operations were performed on a source table, including mapping source columns before iterating through rows.
- Casts were removed from the loops
- Since we can have a n number of XML columns in a file and each bucket can be different, we still iterate over those rows, but only XML columns!
- As a final step, the bulk import table schema is merged into the source table, filling all the missing required columns. It’s quick, since destination table is empty.
if (bucketColumnsPositions.Count > 0)
{
for (var row = 0; row < source.Rows.Count; row++)
{
var xmlBucket = new RateBucketsOverride();
foreach (var idx in bucketColumnsPositions)
{
var cellValue = source.Rows[row].ItemArray[idx].ToString();
if (!string.IsNullOrWhiteSpace(cellValue))
{
xmlBucket.BucketOverrides.Add(
new BucketOverride
{
BucketDescription = source.Columns[idx].ColumnName,
BucketOverrideValue = cellValue
});
}
}
if (xmlBucket.BucketOverrides.Count > 0)
source.Rows[row][_dataSchemaService.ColumnXmlBucket] = ToXml(xmlBucket);
}
}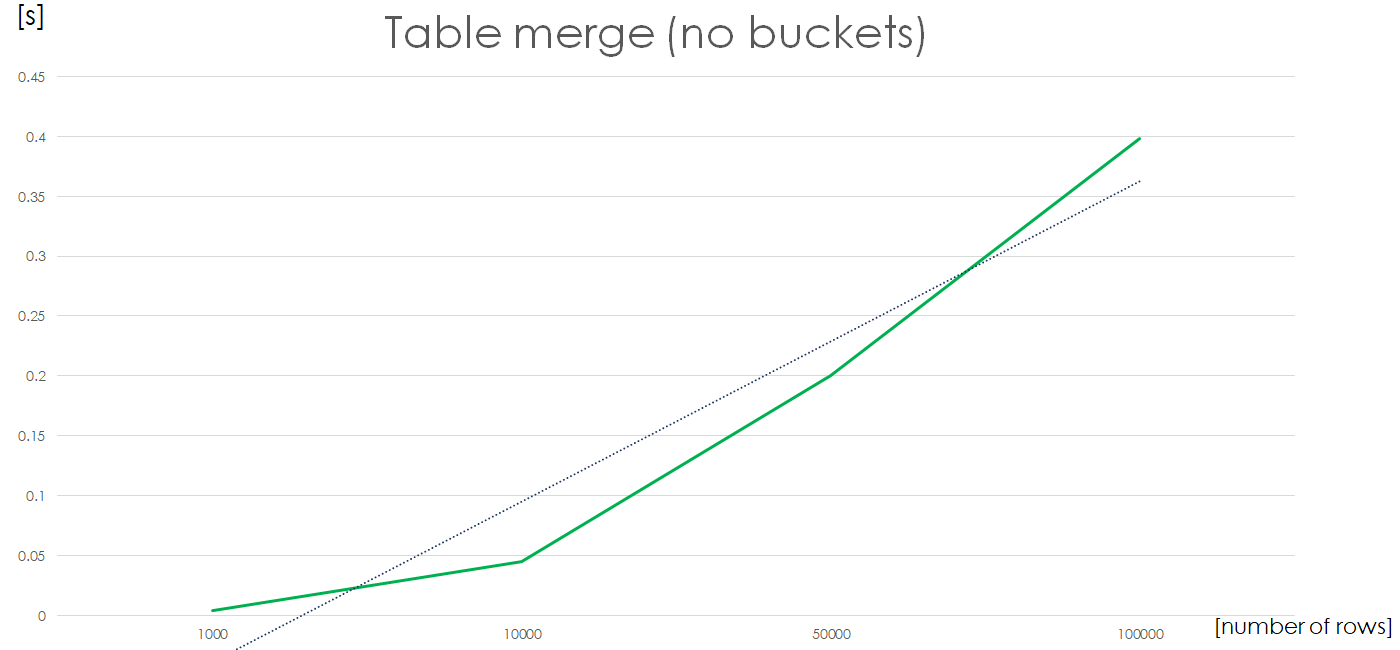
Now the complexity chart looks a lot better. A 2x increase in number of rows in a file results in ~2x increase in calculation time i.e. we have a linear complexity for a file with no XML columns.
Parallel Calculations
Since the number and values of XML columns remain unknown, it’s not possible to further optimize it sequentially as it requires traversing each cell. However, since we are able to link buckets with rest of rows in the DataTable on ID, we can use a parallel calculation.
The issue is that DataTable in C# is thread-safe only for reading, writing to it yields random errors. From the available data structures I picked ConcurrentDictionary as it offers all we need for this task and has a good performance plus offers thread safety.
if (bucketColumnsPositions.Count > 0)
{
Parallel.For(0, source.Rows.Count, (i, row) => {
var xmlBucket = new RateBucketsOverride();
foreach (var idx in bucketColumnsPositions)
{
var cellValue = source.Rows[i].ItemArray[idx].ToString();
if (!string.IsNullOrWhiteSpace(cellValue))
{
xmlBucket.BucketOverrides.Add(
new BucketOverride
{
BucketDescription = source.Columns[idx].ColumnName,
BucketOverrideValue = cellValue
});
}
}
if (xmlBucket.BucketOverrides.Count > 0)
xmlBuckets.TryAdd(i, ToXml(xmlBucket));
});
foreach (var bucket in xmlBuckets)
{
source.Rows[bucket.Key][_dataSchemaService.ColumnXmlBucket] = bucket.Value;
}
}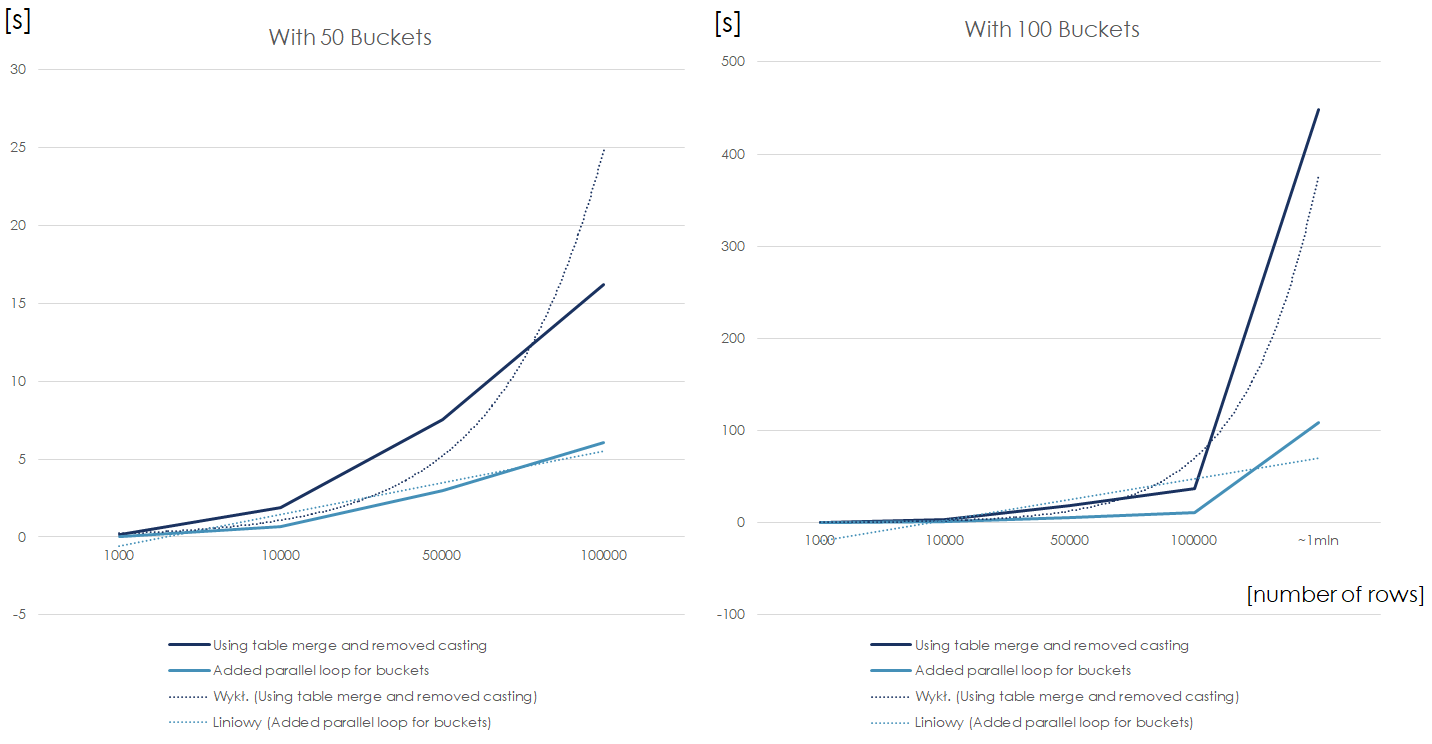
This is a calculation time comparison of the sequential and parallel algorithms using files with 50 and 100 XML columns respectively. We can notice that when the number of rows is drastically higher than number of available threads, the parallel chart breaks the linearity and becomes n (number of rows) * m (number of XML columns above the number of threads).
Thanks to the parallel loops for of XML columns, the growth of calculation time is linear both in terms of number of rows, as well as number of buckets. Precisely, the above is true when number of threads >= number of rows in file, but the reordering service was not a bottleneck anymore.
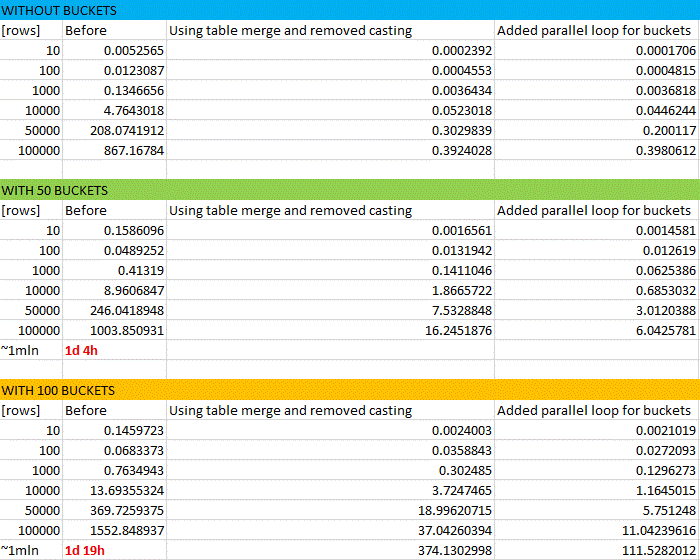
Bonus: here’s the snapshot from real performance tests. The results for 1,000,000 rows were approximated. In a badly written program, it takes almost two days to reorganize 1mln csv rows for an i7 cpu…
Largest region in the matrix – DFS & BFS
If you have or had troubles understanding breath or depth first search, you’ve come to the right place. Here it is – recursive graph search made easy.
Depth-First Search
Depth-first search (DFS) is a method for exploring a graph. In a DFS, you follow the child of traversing node, meaning if the current node has a child, with each step you’ll go deeper into the graph in terms of distance from the root. If a node hasn’t any unvisited children, then go up one level to parent.
Breadth-First Search
Breadth-first search (BFS) is a method for exploring a graph. In a BFS, you first explore all the nodes one step away from the root, then all the nodes two steps away, etc.
The Problem
Consider a matrix with rows and columns, where each cell contains either a ‘0’ or a ‘1’ and any cell containing a 1 is called a filled cell. Two cells are said to be connected if they are adjacent to each other horizontally, vertically, or diagonally. If one or more filled cells are also connected, they form a region. find the length of the largest region.
Input : M[][5] = { 0 0 1 1 0
1 0 1 1 0
0 1 0 0 0
0 0 0 0 1 }
Output : 6
Ex: in the following example, there are 2 regions one with length 1 and the other as 6.
The largest region : 6Is Introduction to Algorithms a good starter?
There are many different approaches to learning algorithms and data structures. However, I’d divide those into two sets: theoretical and practical with all kinds of in-betweens. When I faced this dilemma, I noticed that the most often called title was the famous Introduction to Algorithms by Thomas H. Cormen, Charles E. Leiserson, Ron Rivest, and Clifford Stein. Reading and working through this book took me three months. Let me answer the given question: is Introduction to Algorithms a good starting book for learning algorithms and data structures?
Best of prey problem
The problem:
There are a number of animal species in the forest. Each species has one or more predator that may be direct or indirect. Species X is said to be a predator of species Y if at least or of the following is true:
- Species X is a direct predator of species Y
- If species X is a direct predator of species Z, and Z is a direct predator of Y, then spec is an indirect predator of species Y.
Indirect predation is transitive through any numb of levels. Each species has a maximum of 1 direct predator. No two species will ever be mutual predators, and no species is a predator of itself. Your task is to determine the minimum number of groups that must be formed to so that no species is grouped with its predators, direct or indirect. As an example, consider an array where each position represents a species and each element represents a predator of that species or-1 if there are none. The array is a [-1, 8, 6, 0, 7, 3, 8, 9, -1, 6, 1] and we’ll use zero indexing.
0 8
\ / \
3 1 6
\ / / \
5 10 2 9
\
7
\
4
These are the trees created based on the given array.
The groups will be: [0,8], [3,1,6], [5,10,2,9], [7], [4]We can notice that the asked number of groups without predators is, in fact, the depth of the longers tree branch. Let’s move on directly to the solutions:
Algorithms: Selection sort (JavaScript, PHP)
- Time complexity: O(n2)
Hi, in the second episode of the algorithms series I’d like to take a closer look at yet another simple sorting technique called selection sort. Similarly to bubble sort, it consists of two dependent loops, therefore it’s time complexity also equals to O(n2). It goes like this:
- While sorting the array in ascending order we set the first loop and the first element in the array as a minimum.
- We set up a second loop with a range of the second till the last element, as it doesn’t make much sense to compare the first element with itself.
- If any of the remaining elements in the array is lower than the first, we set it as a minimum.
- As a final step, the lowest value is swapped with the first value (at 0 index).
- The loop continues with j+1 element as a minimum and j+1+1 as the remaining range.
Here’s the presentation (credits to http://www.xybernetics.com):
Algorithms: Bubble sort (JavaScript, PHP)
- Time complexity: O(n2)
Bubble sort is one of the easiest sorting algorithms to implement. The name is derived from the process of sorting based on gradually “bubbling” (or rising) values to their proper location in the array. The bubble sort repeatedly compares adjacent elements of an array as in the following picture:
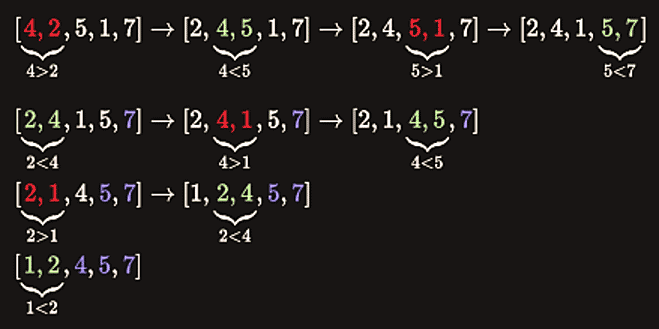
The first and second elements (4 and 2) are compared and swapped if out of order. Then the second and third elements (4 and 5) are compared and swapped if out of order and so on. The algorithm consists of two loops. In each iteration a single value is set in the right place. This sorting process continues until the last two elements of the array are compared and swapped if out of order (the last iteration doesn’t swap any values).



