Is Introduction to Algorithms a good starter?
There are many different approaches to learning algorithms and data structures. However, I’d divide those into two sets: theoretical and practical with all kinds of in-betweens. When I faced this dilemma, I noticed that the most often called title was the famous Introduction to Algorithms by Thomas H. Cormen, Charles E. Leiserson, Ron Rivest, and Clifford Stein. Reading and working through this book took me three months. Let me answer the given question: is Introduction to Algorithms a good starting book for learning algorithms and data structures?
Best of prey problem
The problem:
There are a number of animal species in the forest. Each species has one or more predator that may be direct or indirect. Species X is said to be a predator of species Y if at least or of the following is true:
- Species X is a direct predator of species Y
- If species X is a direct predator of species Z, and Z is a direct predator of Y, then spec is an indirect predator of species Y.
Indirect predation is transitive through any numb of levels. Each species has a maximum of 1 direct predator. No two species will ever be mutual predators, and no species is a predator of itself. Your task is to determine the minimum number of groups that must be formed to so that no species is grouped with its predators, direct or indirect. As an example, consider an array where each position represents a species and each element represents a predator of that species or-1 if there are none. The array is a [-1, 8, 6, 0, 7, 3, 8, 9, -1, 6, 1] and we’ll use zero indexing.
0 8
\ / \
3 1 6
\ / / \
5 10 2 9
\
7
\
4
These are the trees created based on the given array.
The groups will be: [0,8], [3,1,6], [5,10,2,9], [7], [4]We can notice that the asked number of groups without predators is, in fact, the depth of the longers tree branch. Let’s move on directly to the solutions:
Algorithms: Selection sort (JavaScript, PHP)
- Time complexity: O(n2)
Hi, in the second episode of the algorithms series I’d like to take a closer look at yet another simple sorting technique called selection sort. Similarly to bubble sort, it consists of two dependent loops, therefore it’s time complexity also equals to O(n2). It goes like this:
- While sorting the array in ascending order we set the first loop and the first element in the array as a minimum.
- We set up a second loop with a range of the second till the last element, as it doesn’t make much sense to compare the first element with itself.
- If any of the remaining elements in the array is lower than the first, we set it as a minimum.
- As a final step, the lowest value is swapped with the first value (at 0 index).
- The loop continues with j+1 element as a minimum and j+1+1 as the remaining range.
Here’s the presentation (credits to http://www.xybernetics.com):
Algorithms: Bubble sort (JavaScript, PHP)
- Time complexity: O(n2)
Bubble sort is one of the easiest sorting algorithms to implement. The name is derived from the process of sorting based on gradually “bubbling” (or rising) values to their proper location in the array. The bubble sort repeatedly compares adjacent elements of an array as in the following picture:
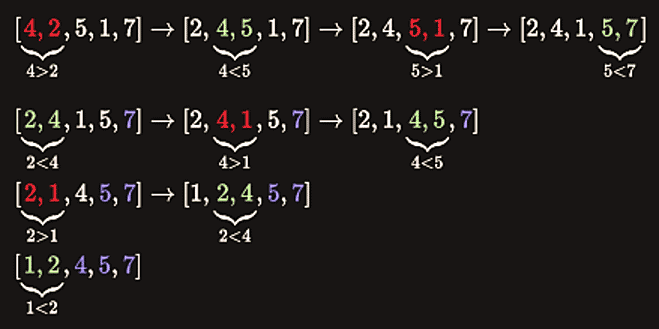
The first and second elements (4 and 2) are compared and swapped if out of order. Then the second and third elements (4 and 5) are compared and swapped if out of order and so on. The algorithm consists of two loops. In each iteration a single value is set in the right place. This sorting process continues until the last two elements of the array are compared and swapped if out of order (the last iteration doesn’t swap any values).

